掌握排列组合核心计算方法，突破数学思维限制，探索无限可能

当数学不再是噩梦

记得高中时第一次接触排列组合,我盯着课本上那堆P和C的符号，脑子里一团乱麻，老师讲得飞快，什么“有序用排列，无序用组合”，我点头假装听懂，其实完全没明白这玩意儿除了考试还能干嘛，直到后来，我偶然用组合数算出了买彩票中奖的概率——低得让人绝望，但那一刻我突然笑了：原来数学真的能解释生活里的那些“可能性”。

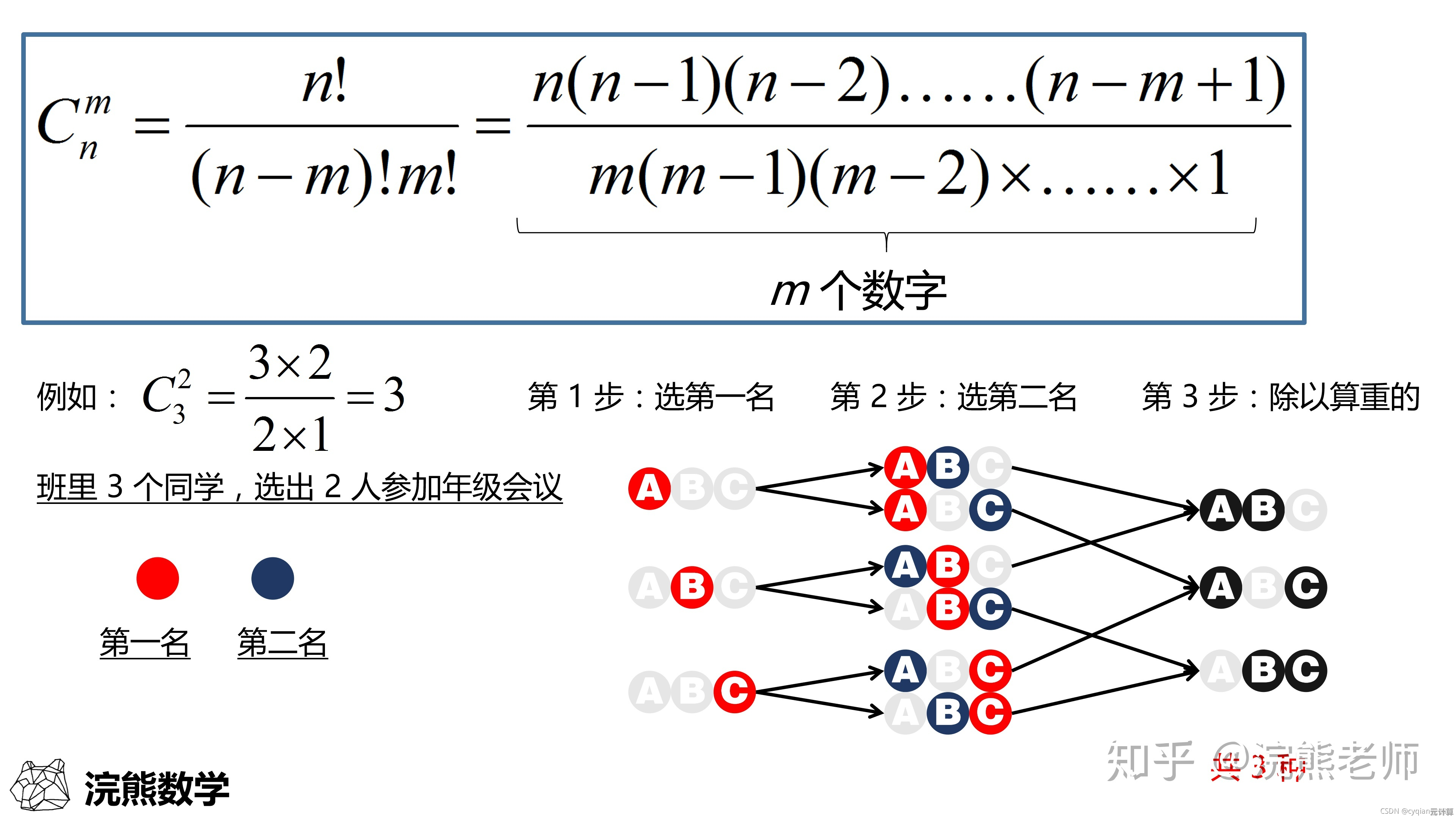
别被公式吓到，先搞懂“为什么”

很多人一上来就背公式：P(n, m)=n!/(n-m)!，C(n, m)=n!/[m!(n-m)!]……但死记硬背只会让你在题目变个花样时立刻懵圈，问“3个学生分5本不同的书，每人至少一本，有几种分法？”如果你硬套公式，可能半天算不出来，但换个思路：先每人分一本保底，剩下2本随意分配——是不是瞬间清晰了？

核心其实是“分类”与“分步”：

• 分类（加法和乘法原理）就像做饭：先决定主食（选米饭或面条），再选菜（炒肉或蒸鱼），每一步选择相乘就是总方案。
• 分步则像拆解任务：比如组密码锁，第一位有10种选择，第二位也有10种……步步相乘。

我常和学生说：排列组合是数学里的“编剧思维”——你得先想象场景中的角色和动作，再决定计算逻辑。

那些坑爹的“特殊情况”才是提分关键

书上不会告诉你,真正卡住人的往往是边界情况。

• “隔板法”算分配方案时，如果允许有人分到零个，要虚拟增加物品数；
• 圆桌排列中,旋转后相同的方案只算一种，得除以人数；
• 数字排列里,0不能当首位，但容易漏算……

有一次我算“7人坐一圈，甲乙必须相邻”的排法，忘了除以7（圆桌特性），结果答案比标准多了一倍，这种错误反而让我记牢了：数学不怕错，怕的是错了不去想为什么。

用生活例子打破抽象墙

排列组合最迷人的是,它能建模真实世界：

• 外卖选“三菜一汤”搭配，其实是组合问题（顺序不影响结果）；
• 手机解锁图案的路径数,是排列（画线顺序不同就算新图案）；
• 甚至谈恋爱——从10个潜在对象里选3个约会，再决定见面顺序，就是先组合后排列……

现实比数学复杂得多（比如人家可能拒绝你），但用数学视角看生活，会多一种“解题”的乐趣。

为什么总觉得自己“想不到”？

很多人卡在排列组合,不是因为笨，而是被“完美思维”绑架了：总想一步到位，怕试错，但这类题的本质就是试错+调整！6本书分三堆，每堆2本”，如果直接套公式容易重复计数，不如手动列举：先选出第一堆，再第二堆……最后除以堆的无序性。

我的经验是：先暴力列举小规模案例，再找规律推广，比如从3本书分堆开始试，很快就能理解为什么公式里要除以3!。

最后一点私心话

学了这么多年数学,我依然会觉得排列组合烦人——尤其是那些嵌套了概率的题，但每次解出答案时，那种“原来如此”的爽感，就像终于拼好了一块纠结已久的拼图。

它教会我的不仅是计算,更是一种思维习惯：世界是由选择和可能性构成的，而数学给了我们工具去量化这种不确定性，哪怕最后算出的答案不完美，但思考的过程本身，已经是在突破自己的边界了。

所以别怕公式,别怕搞错，拿起笔，找张纸，从小案例开始算——错了就划掉重来，数学从来不是天才的游戏，而是每个愿意尝试的人的探险。